How to Calculate Prestress Losses and Jacking Force in a Post-Tensioned Beam

Ques. A “post tensioned” prestressed concrete beam of 50m span is subjected to a transfer prestress force of 9.38 MN. Transfer of force is at 28 days strength. Profile of cable is “parabolic” with maximum eccentricity at mid-span section as 1100mm. Determine the loss of prestress and find the jacking force required. The beam is subjected to a live load of 24 kN/m and jacking is done at both ends of the beam. Use the following data:

Original prestressing force: $P_0 = 9.38$ kN
Area of concrete: $A_c = 947100 mm^2$
Area of steel: $A_s = 8930 mm^2$
Moment of Inertia: $I = 6224 \times 10^8 mm^4$
Anchorage slip: 2.5 mm
Loss due to relaxation of steel: 2%
Creep coefficient: $( C_c = \frac{E_c}{E_e} = 1.2$
Friction coefficient: $\mu = 0.25$
Wobble coefficient: k = 0.0015 /m
Modulus of elasticity of concrete: $E_c = 38.2 GPa$
Modulus of elasticity of steel: $E_s = 210 GPa$
Density of concrete: $24 kN/m^3$

Solution:

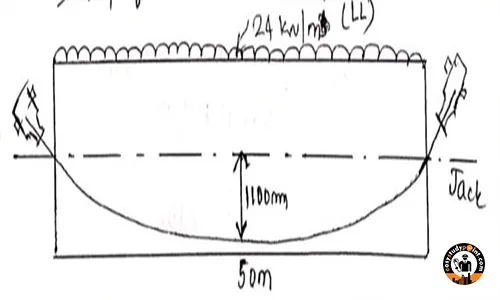
How to Calculate Prestress Losses and Jacking Force in a Post-Tensioned Beam

Initial Prestressing Force= $P_0$ = 9.38 kN = $9.38 \times 10^6 \text{ N}$

Area of Cable (Steel): A= 8930 $mm^2$

Initial Prestress: $\frac{\text{Force}}{\text{Area of cable}}$ ,
= $\frac{9.38 \times 10^6}{8930}$ ,
= $1050.4 \text{N/mm}^2$ ,

Moment of Inertia: $I= 6224 \times 10^8 mm^4$ ,

$f_c = \frac{P}{A} + \frac{P e}{I} e - \frac{M e}{I}$ ,

$f_{c_{\text{support}}} = \frac{P}{A} + 0 - 0$ ,

$f_{c_{\text{support}}} = \frac{9.38 \times 10^6}{947100}$ ,

f_{c_{\text{support}}} = 9.9 \text{ N/mm}^2

f_{c_{\text{midspan}}} = \frac{9.38 \times 10^6}{947100} + \frac{9.38 \times 10^6 \times 1100}{6224 \times 10^8} \times 1100 - \frac{14663.1 \times 10^6 \times 1100}{6224 \times 10^8}

f_{c_{\text{midspan}}} = 2.33 N/mm^2

Average Stress (fc):

${f_c} = 2.33 + \frac{2}{3} (9.9 - 2.33)$ ,
${f_c} = 7.37 N/mm^2$ ,

${Loss} = \phi \cdot f_c \cdot m$
= 1.2×7.37×5.5
= 48.64 N/mm2

Loss Due to Relaxation of Steel

Loss = % of Initial Prestress
% of relaxation of steel = 2\%,

Loss = $\frac{2}{100} \times 1050.4$
=21N/mm2

Loss Due to Anchorage Slip

$Loss = \frac{\Delta E_s}{l}$ ,

$\delta = 2.5 mm \quad \text{(Anchorage slip)}$ ,

${Loss} = \frac{2 \times 2.5 \times 210 \times 10^3}{50 \times 10^3}$ ,

{Loss} = 21 N/mm^2

Loss Due to Friction

When the cable is pulled from both ends

$Slope = \alpha = \frac{4e}{l}$ ,

= $\frac{4 \times 1100}{50 \times 10^3} = 0.088 \quad \text{(Parabolic Cable)}$ ,

x = \frac{l}{2} = \frac{50}{2} = 25 \text{ m}

k = 0.0015 m,

$\mu$ = 0.25

\text{Loss} = P_0 (\mu \alpha + kx)

= $1050.4 \left(0.25 \times 0.088 + 0.0015 \times 25 \right)$

Loss= 62.5 N/mm2

Total Loss of Prestress= 0 + 28.93 + 48.64 + 21 + 21 + 62.5 =181.56 N/mm2

Percentage(%) Loss = $\frac{181.56}{1050.4} \times 100$ = 17.28 %

Calculation of Jacking Force Required

Jacking Force = Initial Prestress + (Total Loss X Area of Cable)

= $(1050.4 + 181.56) \times 8930$
= $11 \times 10^6 \text{ N} [/latex}</p><p>Jacking Force = [latex] 11 X10^6$ N

How to Calculate Prestress Losses and Jacking Force in a Post-Tensioned Beam

Recommended Books:-

Prestressed Concrete: A Fundamental Approach – https://amzn.to/4i7Iy8C
Prestressed Concrete Structures – https://amzn.to/43sQ1un
Design of Prestressed Concrete – https://amzn.to/3DzKR5e

Also Read- Losses In Prestresses- https://engineerlatest.com/losses-in-prestresses/