Calculation of Base & Storey Shear

Design Data

Column = 400 × 400 mm
L/D Ratio = 70
X-Direction Beam = B=230×500 mm
Y-Direction Beam = B=280×750 mm

Project Location

Bengaluru, Zone-II
No. of Floors = 8+G+38 + G + 38+G+3 (Floors) = (4 slabs)

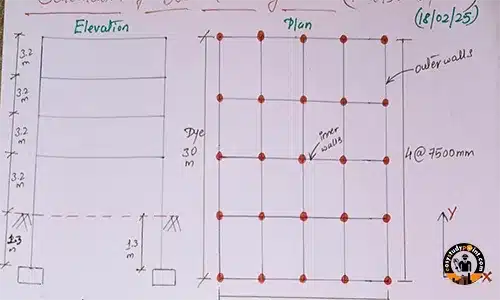
Building Dimensions

Building height is less than 15m, EQM can be used!

Height of the Building = H=14.1H
Width of the Building = W=20 m (DxL))
Length of the Building = L=30 m (Dye)

Wall Details

Outer Walls = t=230 mm
Inner Walls = t=150 mm
Density = 20 $kN/m^3$

Time Period Calculation (Equivalent Static Method)

$T_a = \frac{0.09 h}{\sqrt{d}}$ ,

T_{ay} = \frac{0.09 \times 14.1}{\sqrt{30}} = 0.231 \text{ sec}

Spectral Acceleration, $S_a/g$

$\frac{S_a}{g}$ ,

T_{ax} = 2.5 \text{s}, \quad T_{oy} = 2.5

Refer IS 1893:2016 Cl.no 6.4.2 pg no – 9
For medium stiffness soil sites (0<T<0.55s)

Base Shear Calculation, Vb

V_B = A_h \cdot W

where,

$( V_B )$ = Base Shear,
$( A_h )$ = Horizontal Acceleration Coefficient,
$( W )$ = Seismic Weight

A_h = \left( \frac{Z}{2} \right) \left( \frac{I}{R} \right) \left( \frac{S_a}{g} \right)

Z = 0.10 – Refer to Table 3 pg no.10
I = 1.2- Refer Table 8 Cl.no 7.2.3 pg no – 19
R = 5 – Refer to Table 9 Cl.no 7.2.6 pg no – 20 (RC buildings with SMRF)

$A_h = \left( \frac{0.10}{2} \right) \times \left( \frac{1.2}{5} \right) \times 2.5 = 0.03$ (Max. horizontal acceleration coefficient)

Seismic Weight Calculation (175mm THK Slab)

Slab area/floor:
x=20+0.2+0.2=20.4m
y=30+0.2+0.2=30.4my
Area=20.4×30.4=620.16≈621m2

1) Self-weight of slab per floor

= 25 kN/m3×(621×0.175)m3 =2716.88 kN

2) Floor Finish Load per floor

=1.5 kN/m2×(621)m3
=931.5 kN

3) Live Load (3 kN/m²) (Reduced L.L)

= 0.25×3 kN/m2×(621)m2
=465.75≈466 kN

Total Load

=1115 kN/floor

(Refer IS 1893:2016 Table-10 Cl. 7.3.1 pg no – 20)

Beam weight calculation

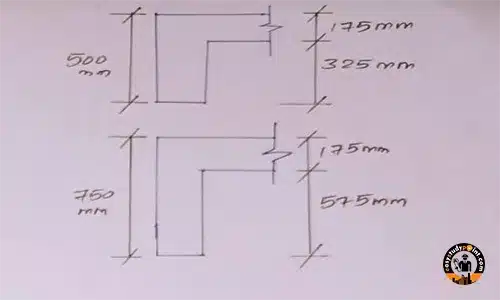
Self-weight of beam

= 25 kN/m³ × (0.325 × 0.225 × 0.4) × 5
= 0.3
(Along x-beam)

(0.55 × 3.0 × 1.5)
(Along y-beam)

= 25 kN/m³ × (33.15 + 87.4) m³
= 25 × 0.3 × (3.15 + 8.94)
= 904 + 125
= 905 kN/floor

Masonry wall calculation

Outer wall load (20% opening/storey)

Self-weight of outer walls =

= 20 kN/m³ × 0.23 × 0.8 ×{(3.2 – 0.5) × 20.4 × 2 + (3.2 – 0.25) × 30.4 × 2}
(Along x-axis) (Along y-axis)

= 20 × 0.23 × 0.8 × (10.16 + 148.92)
= 20 × 0.23 × 0.8 × 259.12
= 953.56
≈ 954 kN

Inner wall load (20% opening/storey)

Self-weight of inner wall =

= 20 kN/m³ × 0.115 × 0.8 ×{(3.2 – 0.5) × 20.4 × 3 + (3.2 – 0.25) × 30.4 × 3}
(Along x-axis) (Along y-axis)

= 20 × 0.115 × 0.8 × (165.24 + 223.44)
= 715.17 kN
≈ 716 kN

Total weight of wall/storey = 954 + 716 = 1670 kN

Self-weight in GL/1st storey
- [/latex] \frac{1670}{2} = 835 \text{ kN} $</li> </ul> </li><li><strong>Self-weight in the 2nd storey</strong> <ul class="wp-block-list"> <li>$ \frac{1670 + 1670}{2} = 1670 \text{ kN} [/latex]
Self-weight in the 3rd storey
- $\frac{1670 + 1670}{2} = 1670 \text{ kN}$
Self-weight in the 4th storey
- $\frac{1670}{2} = 835 \text{ kN}$

Column weight calculation

Self-weight of all 30 columns (GL/1st storey)
- = $25{ kN/m}^3 \times 0.4 \times 0.4 \times \left( \frac{4.5}{2} + \frac{3.2}{2} \right) \times 25$
  = $25 \times 0.4 \times 0.4 \times 96.25$
  =385kN
Self-weight of all columns in the 2nd storey
- = $25{ kN/m}^3 \times 0.4 \times 0.4 \times \left( \frac{3.2}{2} + \frac{3.2}{2} \right) \times 25$
  = 320kN
Self-weight of all columns in the 3rd storey
- = $25 \text{ kN/m}^3 \times 0.4 \times 0.4 \times \left( \frac{3.2}{2} + \frac{3.2}{2} \right) \times 25$
  =320kN
Self-weight of all columns in the 4th storey
- = $25 \text{ kN/m}^3 \times 0.4 \times 0.4 \times \left( \frac{3.2}{2} \right) \times 25$
  =160kN

Seismic weight calculation per storey

Seismic weight = Slab load + Beam load + Wall load + $\frac{\text{Column load}}{\text{floor}}$

Seismic weight of the Ground storey-
= W1 = 4115 + 905 + 835 + 385
= 6240kN
Seismic weight of the 2nd storey
= W2 = 4115 + 905 + 1670 + 320
= 7010kN
Seismic weight of 3rd storey
=W3 = 4115 + 905 + 1670 + 320
=7010kN
Seismic weight of 4th storey
=W4 = 4115 + 905 + 835 + 160
= 6015kN

Total seismic weight (W)= W = W1 + W2 + W3 + W4
= 6240 + 7010 + 7010 + 6015
= 26275 kN

$V_B = Ah x w$
$V_B$ = 0.03 x 26275 =78.25kN

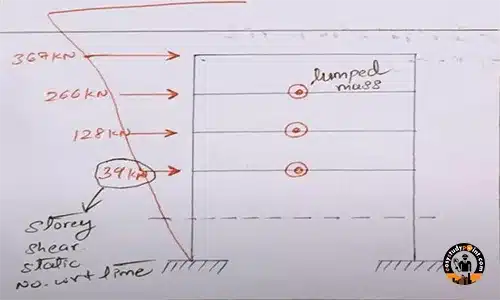
(Distribute this base shear to every storey/floor level)

Storey Shear Calculation: (Q)

h1 = 4.5m,
h2 = 4.5 + 3.2 = 7.7m
h3 = 7.7 + 3.2 = 10.9m,
h4 = 10.9 + 3.2 = 14.1m

Design Lateral Force (Q)

$Q_i = \frac{W_i h_i^2}{\sum\limits_{j=1}^{n} W_j h_j^2} \times V_B$ , (Refer IS1893:2016 part 1 Pgno.23)

Q_1 = \frac{W_1 h_1^2}{W_1 h_1^2 + W_2 h_2^2 + W_3 h_3^2 + W_4 h_4^2} \times V_B

Q_1 = \frac{(6240 \times 4.5^2) + (7010 \times 7.7^2) + (7010 \times 10.9^2) + (6015 \times 14.1^2)}{126360 + 415622.9 + 832858.1 + 1195842} \times 788.25

Q_1 = \frac{126360}{126360 + 415622.9 + 832858.1 + 1195842} \times 788.25

Q_1 = 38.74 kN

Q_2 = \frac{W_2 h_2^2}{W_1 h_1^2 + W_2 h_2^2 + W_3 h_3^2 + W_4 h_4^2} \times V_B

Q_2 = \frac{7010 \times 7.7^2}{(6240 \times 4.5^2) + (7010 \times 7.7^2) + (7010 \times 10.9^2) + (6015 \times 14.1^2)} \times 788.25

Q2= 127.44kN

Q_3 = \frac{W_3 h_3^2}{W_1 h_1^2 + W_2 h_2^2 + W_3 h_3^2 + W_4 h_4^2} \times V_B

Q_3 = \frac{7010 \times 10.9^2}{(6240 \times 4.5^2) + (7010 \times 7.7^2) + (7010 \times 10.9^2) + (6015 \times 14.1^2)} \times 788.25

Q3= 255.38kN

Q_4 = \frac{W_4 h_4^2}{W_1 h_1^2 + W_2 h_2^2 + W_3 h_3^2 + W_4 h_4^2} \times V_B

Q4 = 366.68

Recommended Books:-

1. “Dynamics of Structures: Theory and Applications to Earthquake Engineering” – https://amzn.to/41GhwPU
2. “Earthquake Resistant Design of Structures”- https://amzn.to/3F5jbWn
3. “Structural Dynamics: Theory and Computation” – https://amzn.to/3XlVvTN
4. Seismic Design of Reinforced Concrete and Masonry Buildings – https://amzn.to/3Dt7PLj

Also read:- Staircase Basics, Design, Components, Types, and Safety Standards