How to Calculate Prestress Losses and Jacking Force in a Post-Tensioned Beam
Table of Contents
Ques. A “post tensioned” prestressed concrete beam of 50m span is subjected to a transfer prestress force of 9.38 MN. Transfer of force is at 28 days strength. Profile of cable is “parabolic” with maximum eccentricity at mid-span section as 1100mm. Determine the loss of prestress and find the jacking force required. The beam is subjected to a live load of 24 kN/m and jacking is done at both ends of the beam. Use the following data:
Original prestressing force: P_0 = 9.38 kN
Area of concrete: A_c = 947100 mm^2
Area of steel: A_s = 8930 mm^2
Moment of Inertia: I = 6224 \times 10^8 mm^4
Anchorage slip: 2.5 mm
Loss due to relaxation of steel: 2%
Creep coefficient: ( C_c = \frac{E_c}{E_e} = 1.2
Friction coefficient: \mu = 0.25
Wobble coefficient: k = 0.0015 /m
Modulus of elasticity of concrete: E_c = 38.2 GPa
Modulus of elasticity of steel: E_s = 210 GPa
Density of concrete: 24 kN/m^3
Solution:
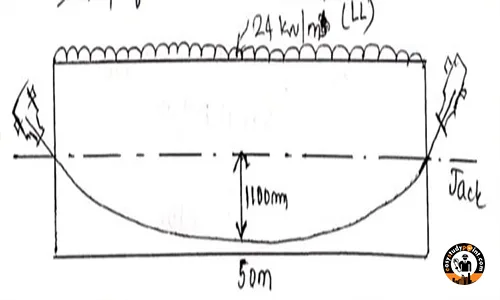
Initial Prestressing Force= P_0 = 9.38 kN = 9.38 \times 10^6 \text{ N}
Area of Cable (Steel): A= 8930 mm^2
Initial Prestress: \frac{\text{Force}}{\text{Area of cable}} ,
= \frac{9.38 \times 10^6}{8930} ,
= 1050.4 \text{N/mm}^2 ,
Moment of Inertia: I= 6224 \times 10^8 mm^4 ,
f_c = \frac{P}{A} + \frac{P e}{I} e - \frac{M e}{I} ,
f_{c_{\text{support}}} = \frac{P}{A} + 0 - 0 ,
f_{c_{\text{support}}} = \frac{9.38 \times 10^6}{947100} ,
f_{c_{\text{support}}} = 9.9 \text{ N/mm}^2 f_{c_{\text{midspan}}} = \frac{9.38 \times 10^6}{947100} + \frac{9.38 \times 10^6 \times 1100}{6224 \times 10^8} \times 1100 - \frac{14663.1 \times 10^6 \times 1100}{6224 \times 10^8} f_{c_{\text{midspan}}} = 2.33 N/mm^2- Average Stress (fc):
{f_c} = 2.33 + \frac{2}{3} (9.9 - 2.33) ,
{f_c} = 7.37 N/mm^2 ,
{Loss} = \phi \cdot f_c \cdot m
= 1.2×7.37×5.5
= 48.64 N/mm2
- Loss Due to Relaxation of Steel
Loss = % of Initial Prestress
% of relaxation of steel = 2\%,
Loss = \frac{2}{100} \times 1050.4
=21N/mm2
- Loss Due to Anchorage Slip
Loss = \frac{\Delta E_s}{l} ,
\delta = 2.5 mm \quad \text{(Anchorage slip)} ,
{Loss} = \frac{2 \times 2.5 \times 210 \times 10^3}{50 \times 10^3} ,
{Loss} = 21 N/mm^2- Loss Due to Friction
When the cable is pulled from both ends
Slope = \alpha = \frac{4e}{l} ,
= \frac{4 \times 1100}{50 \times 10^3} = 0.088 \quad \text{(Parabolic Cable)} ,
x = \frac{l}{2} = \frac{50}{2} = 25 \text{ m}k = 0.0015 m,
\mu = 0.25
\text{Loss} = P_0 (\mu \alpha + kx)= 1050.4 \left(0.25 \times 0.088 + 0.0015 \times 25 \right)
Loss= 62.5 N/mm2
Total Loss of Prestress= 0 + 28.93 + 48.64 + 21 + 21 + 62.5 =181.56 N/mm2
Percentage(%) Loss = \frac{181.56}{1050.4} \times 100 = 17.28 %
- Calculation of Jacking Force Required
Jacking Force = Initial Prestress + (Total Loss X Area of Cable)
= (1050.4 + 181.56) \times 8930
= 11 \times 10^6 \text{ N} [/latex}</p><p>Jacking Force = [latex] 11 X10^6 N
How to Calculate Prestress Losses and Jacking Force in a Post-Tensioned Beam
Recommended Books:-
- Prestressed Concrete: A Fundamental Approach – https://amzn.to/4i7Iy8C
- Prestressed Concrete Structures – https://amzn.to/43sQ1un
- Design of Prestressed Concrete – https://amzn.to/3DzKR5e
Also Read- Losses In Prestresses- https://engineerlatest.com/losses-in-prestresses/











1 comment